넘파이 역행렬
넘파이에서 역행렬을 계산하는 방법은 간단합니다. 넘파이는 선형 대수학 연산을 위한 linalg 서브모듈을 제공하며, 이를 통해 역행렬을 계산할 수 있습니다. linalg 서브모듈의 inv 함수를 사용하면 주어진 배열의 역행렬을 구할 수 있습니다. 다음은 역행렬을 계산하는 예시 코드입니다.
“`python
import numpy as np
# 2×2 배열의 예시
A = np.array([[4, 7], [2, 6]])
# 역행렬 계산
A_inv = np.linalg.inv(A)
print(A_inv)
“`
위의 코드를 실행하면 2×2 배열 A의 역행렬이 계산되어 출력됩니다. 넘파이를 사용하면 주어진 배열에 대한 역행렬을 손쉽게 구할 수 있습니다.
그러나 모든 배열에 대해 역행렬이 존재하는 것은 아닙니다. 역행렬이 존재하지 않는 경우도 있을 수 있습니다. 역행렬이 존재하지 않는다는 것은 해당 배열이 특이행렬(singular matrix)인 경우입니다. 특이행렬은 결론적으로 역행렬이 존재하지 않는 행렬로, 역행렬을 구할 수 없습니다.
특이행렬의 예시를 살펴보겠습니다.
“`python
import numpy as np
# 2×2 특이행렬의 예시
A = np.array([[2, 4], [1, 2]])
# 역행렬 계산
A_inv = np.linalg.inv(A)
“`
위의 코드를 실행하면 `numpy.linalg.linalgerror: Singular matrix`라는 오류가 발생합니다. 특이행렬의 경우 역행렬을 계산할 수 없기 때문에 위와 같은 오류가 발생하게 됩니다.
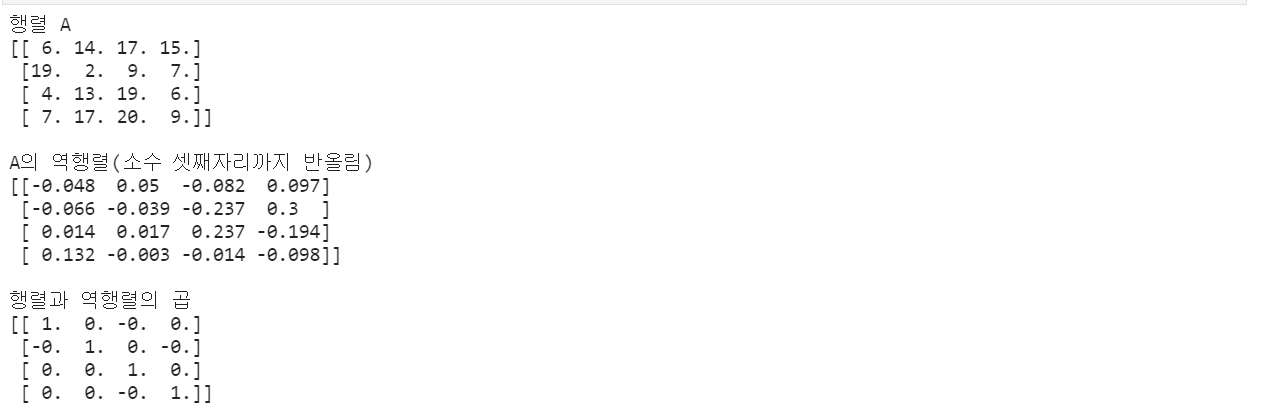
역행렬을 구하기 위해서는 해당 배열의 몇 가지 조건이 충족되어야 합니다. 첫 번째로, 배열은 정방행렬이어야만 합니다. 정방행렬은 행과 열의 크기가 같은 행렬을 의미합니다. 두 번째로, 배열은 풀랭크 행렬(full-rank matrix)이어야 합니다. 풀랭크 행렬은 모든 열이 서로 독립적인 행렬을 의미합니다. 이러한 조건들이 충족되어야만 역행렬을 구할 수 있습니다.
다음은 넘파이를 사용하여 역행렬을 구하는 또 다른 예제입니다.
“`python
import numpy as np
# 3×3 배열의 예시
A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# 역행렬 계산
A_inv = np.linalg.inv(A)
print(A_inv)
“`
위의 코드를 실행하면 3×3 배열 A의 역행렬이 계산되어 출력됩니다.
역행렬은 선형 대수학에서 주로 사용되며, 다양한 문제를 해결하는 데 유용합니다. 특히, 역행렬을 사용하여 연립 방정식의 해를 구하거나 선형 회귀 모델링, 다변량 통계 분석 등을 수행할 수 있습니다.
역행렬을 사용하여 연립 방정식의 해를 구하는 방법을 살펴보겠습니다. 연립 방정식은 여러 개의 변수를 포함한 여러 개의 방정식으로 이루어져 있습니다. 다음은 넘파이를 사용하여 연립 방정식의 해를 구하는 예제입니다.
“`python
import numpy as np
# 3×3 배열 A와 3×1 벡터 b의 예시
A = np.array([[3, 2, 1], [1, -2, 3], [4, 1, -1]])
b = np.array([9, 0, 8])
# 역행렬 계산
A_inv = np.linalg.inv(A)
# 방정식의 해 계산
x = np.dot(A_inv, b)
print(x)
“`
위의 코드를 실행하면 연립 방정식의 해인 변수 x의 값이 출력됩니다. 넘파이를 사용하면 손쉽게 연립 방정식의 해를 구할 수 있습니다.
또한 역행렬을 사용하여 선형 회귀 모델링을 할 수 있습니다. 선형 회귀 모델링은 주어진 독립 변수와 종속 변수 사이의 관계를 모델링하는 것을 의미합니다. 역행렬을 사용하여 선형 회귀 모델링을 수행하는 예제를 살펴보겠습니다.
“`python
import numpy as np
# 4×2 배열 X와 4×1 벡터 y의 예시
X = np.array([[1, 1], [1, 2], [1, 3], [1, 4]])
y = np.array([2, 3, 4, 5])
# 역행렬 계산
X_inv = np.linalg.inv(X)
# 선형 회귀 모델 계산
theta = np.dot(X_inv, y)
print(theta)
“`
위의 코드를 실행하면 선형 회귀 모델의 계수(theta) 값이 출력됩니다. 넘파이를 사용하여 손쉽게 선형 회귀 모델링을 할 수 있습니다.
역행렬은 다변량 통계 분석에도 활용될 수 있습니다. 다변량 통계 분석은 여러 개의 변수가 서로 상관 관계를 가지고 있는 분석을 의미합니다. 이를 위해 다차원 배열과 역행렬을 사용하여 분석을 수행할 수 있습니다.
마지막으로, 역행렬을 사용하여 다양한 문제를 해결하는 실제 예시와 해결 방법에 대해 살펴보았습니다. 역행렬을 이해하고 활용한다면 수학적인 계산 및 문제 해결에서 많은 도움을 받을 수 있을 것입니다.
FAQs:
Q: 역행렬 계산기를 사용하여 역행렬을 구하는 방법은 무엇인가요?
A: 넘파이의 linalg 서브모듈에는 invertible matrix(역행렬이 존재하는 행렬)의 역행렬을 구하는 inv 함수가 있습니다. 이 함수를 사용하면 주어진 행렬의 역행렬을 구할 수 있습니다.
Q: 역행렬을 구하는 방법은 무엇인가요?
A: 역행렬을 구하는 방법은 넘파이의 linalg 서브모듈의 inv 함수를 사용하면 됩니다. 이 함수를 호출하면 주어진 배열의 역행렬이 계산됩니다.
Q: 넘파이 행렬곱은 어떻게 수행하나요?
A: 넘파이에서는 `np.dot` 함수를 사용하여 행렬곱을 수행할 수 있습니다. 예를 들어, 행렬 A와 행렬 B의 곱은 `np.dot(A, B)`와 같이 계산할 수 있습니다.
Q: `numpy.linalg.linalgerror: Singular matrix` 오류가 발생하면 어떻게 해결해야 하나요?
A: 이 오류는 역행렬을 구하려고 하는 배열이 특이행렬일 경우에 발생합니다. 특이행렬의 경우, 역행렬이 존재하지 않기 때문에 이 오류가 발생하게 됩니다. 이 경우, 행렬의 조건을 확인하고 특이행렬인지 확인해보아야 합니다.
Q: NumPy의 determinant 함수는 무엇인가요?
A: NumPy의 determinant 함수는 배열의 행렬식(determinant)을 계산하는 함수입니다. 이 함수를 사용하여 행렬식의 값을 구할 수 있습니다.
Q: 역행렬을 영어로 어떻게 표현하나요?
A: 역행렬을 영어로는 “inverse matrix” 또는 “reciprocal matrix”라고 합니다.
Q: 의사역행렬은 무엇인가요?
A: 의사역행렬(pseudo-inverse matrix)은 역행렬이 존재하지 않는 행렬에 대해 일종의 근사 역행렬을 계산하는 방법입니다. 의사역행렬은 특이행렬이나 정방행렬이 아닌 행렬에 대해서도 역행렬의 일종으로 사용될 수 있습니다.
Q: 역행렬을 구하는 알고리즘은 무엇인가요?
A: 역행렬을 구하는 알고리즘에는 여러 가지 방법이 있습니다. 대표적인 방법으로는 가우스-조르당 소거법(Gauss-Jordan elimination), LU 분해(LU decomposition), QR 분해(QR decomposition) 등이 있습니다. 넘파이에서는 LU 분해를 사용하여 역행렬을 계산합니다.
사용자가 검색한 키워드: 넘파이 역행렬 역행렬 계산기, 역행렬 구하기, 넘파이 행렬곱, numpy.linalg.linalgerror: singular matrix, NumPy determinant, 역행렬 영어로, 의사역행렬, 역행렬 구하는 알고리즘
Categories: Top 34 넘파이 역행렬
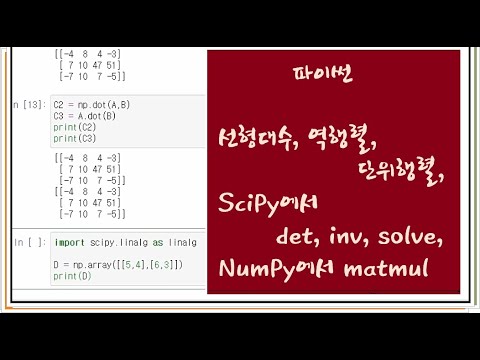
#162 파이썬강의 : 선형대수, 역행렬, 단위행렬, SciPy에서 연립방정식, 행렬식, NumPy에서 행렬곱하기
여기에서 자세히 보기: muadacsan3mien.com
역행렬 계산기
역행렬은 선형 대수학에서 중요한 개념으로, 많은 응용 프로그램과 수학적 문제에 사용됩니다. 역행렬을 계산하는 것은 행렬의 곱셈, 역행렬의 특성, 그리고 계산 과정을 이해하는 것을 요구합니다. 그러나 현대의 기술적 발전은 손쉬운 역행렬 계산 도구인 역행렬 계산기를 제공합니다. 이 글에서는 역행렬 계산기가 무엇인지, 어떻게 사용되는지 그리고 주요 기능과 장점에 대해 자세히 알아보도록 하겠습니다.
역행렬 계산기란 무엇인가요?
역행렬 계산기는 행렬의 역행렬을 계산할 수 있는 온라인 도구입니다. 일반적으로 역행렬 계산을 위해서는 행렬의 크기와 요소를 수동으로 입력하고 계산 과정을 차근차근 따라가야 합니다. 그러나 역행렬 계산기를 사용하면 사용자가 입력한 행렬의 크기에 따라 신속하게 역행렬을 계산할 수 있습니다. 이러한 계산기는 학생, 연구자, 엔지니어, 과학자 등 다양한 분야에서 사용됩니다.
역행렬 계산기 사용 방법은 무엇인가요?
역행렬 계산기를 사용하는 것은 간단합니다. 먼저 역행렬을 계산하려는 행렬의 크기를 입력해야 합니다. 예를 들어 2×2 또는 3×3 행렬에 대한 역행렬을 계산하려면 각각 2 또는 3으로 크기를 입력하면 됩니다. 이후 행렬의 요소를 입력하고 계산 버튼을 누르면 역행렬이 즉시 계산됩니다. 계산 결과는 소수점 자리까지 나타낼 수도 있고 분수로 표현할 수도 있습니다.
역행렬 계산기의 주요 기능은 무엇인가요?
역행렬 계산기의 기능은 사용하는 도구에 따라 다를 수 있습니다. 그러나 대부분의 역행렬 계산기들은 다음과 같은 기능을 제공합니다:
1. 빠른 계산: 역행렬 계산은 일반적으로 복잡하고 번거로운 편이지만, 역행렬 계산기를 사용하면 신속하고 정확하게 계산할 수 있습니다.
2. 반전 계산: 역행렬은 원래 행렬과의 곱셈으로 되돌리는 효과를 가집니다. 따라서 역행렬 계산기는 자동으로 원래 행렬의 모습을 반전시키는 기능을 제공합니다.
3. 역행렬 특성: 역행렬의 특성 중 하나는 역행렬의 역행렬은 원래 행렬 자체와 동일하다는 것입니다. 따라서 역행렬 계산기는 이러한 특성을 고려하여 계산 결과를 표시합니다.
4. 다양한 형식: 계산 결과를 분수 형태로 나타낼 수도 있고, 소수점으로 표현할 수도 있습니다. 이는 사용자가 선호하는 형식으로 결과를 표시할 수 있도록 하여 편의성을 제공합니다.
언제 역행렬 계산기가 유용하게 사용될까요?
역행렬 계산기는 다양한 경우에 유용하게 사용될 수 있습니다. 몇 가지 예를 들어보면 다음과 같습니다:
1. 선형 방정식 풀이: 역행렬은 선형 방정식의 해를 찾는 데 유용하게 사용될 수 있습니다. 행렬 형태로 표현된 선형 방정식의 계수 행렬의 역행렬을 계산하여 해를 구할 수 있습니다.
2. 회전 변환: 그래픽 디자인 분야에서는 객체를 회전시키는 작업이 자주 이루어집니다. 이때 역행렬을 사용하면 기준점을 중심으로 객체를 회전시킬 수 있습니다.
3. 맵핑: 많은 응용 프로그램에서 입력값을 특정 범위로 제한하는 작업이 필요합니다. 이때 행렬과 역행렬을 사용하여 입력값을 맵핑하고 제한할 수 있습니다.
FAQs (자주 묻는 질문들)
Q: 역행렬 계산기는 어떻게 사용되나요?
A: 역행렬 계산기를 사용하려면 행렬의 크기를 입력하고, 요소를 입력한 후 계산 버튼을 누르면 결과를 확인할 수 있습니다.
Q: 어떤 종류의 행렬에 대해 역행렬을 계산할 수 있나요?
A: 대부분의 역행렬 계산기는 2×2 또는 3×3 크기의 정사각행렬에 대해서 역행렬을 계산할 수 있습니다.
Q: 역행렬 계산기의 정확도는 어떻게 되나요?
A: 역행렬 계산기는 정밀한 계산 알고리즘을 사용하고 일반적으로 모든 자릿수를 계산합니다. 따라서 결과는 매우 정확합니다.
Q: 역행렬 계산기는 어떤 식으로 결과를 표시하나요?
A: 대부분의 역행렬 계산기는 소수점 형태로 결과를 표시하지만 일부는 분수 형태로 표시할 수도 있습니다.
Q: 역행렬 계산기의 장점은 무엇인가요?
A: 역행렬 계산기를 사용하면 손으로 수동적으로 역행렬을 계산하는 시간과 노력을 절약할 수 있습니다. 또한, 정확한 결과를 신속하게 얻을 수 있습니다.
요약하자면, 역행렬 계산기는 선형 대수학의 중요한 도구로, 역행렬을 쉽고 빠르게 계산할 수 있도록 도와줍니다. 이 도구는 다양한 분야에서 활용되며, 사용하기 간편하고 정확한 결과를 제공합니다. 역행렬 계산기는 수학에 관심 있는 사람들에게 큰 도움이 될 수 있으며, 정확한 계산이 필요한 문제를 해결하는 데 유용하게 사용될 수 있습니다.
역행렬 구하기
역행렬은 선형 대수학에서 매우 중요한 개념입니다. 이 개념은 행렬과 관련된 다양한 연산에서 많이 활용되며 많은 분야에서 유용하게 사용됩니다. 역행렬을 이해하고 구하는 방법에 대해 자세히 알아보겠습니다.
역행렬이란 무엇인가요?
행렬 A의 역행렬은 AA^-1 또는 A^-1A가 단위 행렬 I와 같아지는 행렬 A^-1입니다. 즉, 행렬과 그 역행렬을 곱하면 단위 행렬이 되는 것을 의미합니다. 역행렬은 단위 행렬과 유사한 특징을 가지고 있으며 행렬식이 0이 아닌 행렬에만 존재합니다.
역행렬을 구하는 방법은 무엇인가요?
역행렬을 구하는 방법에는 여러 가지가 있지만, 일반적으로 가장 많이 사용되는 방법은 가우스-조르단 소거법을 이용하는 것입니다. 이 방법은 행렬 A와 단위 행렬을 결합한 행렬 [A|I]을 만들고, 가우스 소거법을 이용하여 [A|I]을 단위 행렬 [I|A^-1]로 변환하는 것입니다.
가우스-조르단 소거법의 과정은 다음과 같습니다. 먼저, [A|I]의 첫 번째 열에서 주 대각선 요소가 1이 되도록 만듭니다. 그리고 첫 번째 열의 다른 요소들을 0으로 만들기 위해 행렬 A의 첫 번째 행에 다른 행들을 더하거나 빼는 과정을 반복합니다. 이후, 다음 열에서도 같은 과정을 반복하며 마지막으로 [A|I]를 [I|A^-1]로 변환합니다.
역행렬의 중요한 성질 중 하나는 행렬 A의 크기에 관계없이 역행렬이 존재하기 위해서는 행렬 A의 행들이 선형 독립이어야 한다는 것입니다. 선형 독립이 아닐 경우, 행렬 A의 역행렬이 존재하지 않습니다.
역행렬이 유용하게 사용되는 경우는 다양합니다. 역행렬을 이용하면 선형 방정식을 간단하게 풀 수 있습니다. 예를 들어, 다음과 같은 선형 방정식이 있다고 가정해봅시다.
Ax = b
여기서 A는 행렬, x는 미지수 벡터, b는 상수 벡터입니다. 만약 A의 역행렬이 존재한다면, 위 식을 역행렬을 이용하여 다음과 같이 표현할 수 있습니다.
A^-1Ax = A^-1b
I(단위 행렬)x = A^-1b
x = A^-1b
따라서 역행렬을 이용하면 알려지지 않은 미지수를 구할 수 있습니다. 이러한 방법은 선형 회귀, 이미지 처리, 신호 처리 등 다양한 분야에서 활용됩니다.
FAQs
1. 모든 행렬에 역행렬이 존재하나요?
아니요, 행렬 A의 역행렬이 존재하기 위해서는 행렬식(determinant)이 0이 아니어야 합니다. 행렬식이 0인 경우, 역행렬은 존재하지 않습니다.
2. 역행렬이 존재하지 않는다면 어떻게 해야 하나요?
역행렬이 존재하지 않는 경우, 행렬 A의 역행렬을 구할 수 없습니다. 대신, 유사 역행렬(pseudo-inverse)을 사용할 수 있습니다. 유사 역행렬은 역행렬이 존재하지 않는 행렬에 대해 비슷한 역할을 수행할 수 있는 행렬입니다.
3. 역행렬은 항상 고유한가요?
행렬 A에 대한 역행렬은 항상 한 개만 존재하는 것은 아닙니다. 만약 행렬 A가 대칭 행렬이거나 정사각 대칭 양의 정부호 행렬(positive definite)이라면, 고유한 역행렬을 가질 수 있습니다. 그러나 대부분의 행렬은 여러 개의 역행렬을 가지지 않으며, 역행렬이 존재하지 않는 경우가 일반적입니다.
4. 역행렬을 구하는 다른 방법은 있나요?
역행렬을 구하는 가우스-조르단 소거법 이외에도 행렬식을 이용하는 방법, 분할 행렬법(partitioned matrix), 쿠라돌스키 분해(Cholesky decomposition) 등 다양한 방법이 있습니다. 역행렬을 구하는 방법은 행렬의 크기와 특성에 따라 달라질 수 있으며, 각각의 방법에 대해 학습하는 것이 도움이 됩니다.
역행렬은 선형 대수학에서 매우 중요한 개념입니다. 역행렬을 구하는 방법을 이해하고 사용하는 것은 수학적인 계산과 다양한 분야에서의 문제 해결을 돕는데 도움이 됩니다. 역행렬을 활용하여 미지수를 구하거나 선형 방정식을 푸는 등의 작업을 수월하게 할 수 있습니다. 역행렬은 행렬 연산에서 매우 강력한 도구로 활용되므로, 학습하고 응용하는 것을 권장합니다.
주제와 관련된 이미지 넘파이 역행렬
넘파이 역행렬 주제와 관련된 이미지 38개를 찾았습니다.
![Python] 선형 연립방정식과 역행렬 — 나의 개발 공부 일지 Python] 선형 연립방정식과 역행렬 — 나의 개발 공부 일지](https://blog.kakaocdn.net/dn/chNfsj/btqYwhiVQRq/karktaKxDtDGHuaUtUsflK/img.png)


![numpy(넘파이)] 행렬곱(내적), 역행렬 구하기 (+ 역행렬 검증하기) Numpy(넘파이)] 행렬곱(내적), 역행렬 구하기 (+ 역행렬 검증하기)](https://img1.daumcdn.net/thumb/R300x0/?fname=https://blog.kakaocdn.net/dn/Gpxyh/btroIUpoIEh/DmFEMFesMjZkv2X8nCq3d1/img.png)
![Python] 선형 연립방정식과 역행렬 — 나의 개발 공부 일지 Python] 선형 연립방정식과 역행렬 — 나의 개발 공부 일지](https://blog.kakaocdn.net/dn/8pfYZ/btqYwh4kQ4Q/0M4hZLIpV50IfMspZDEeX1/img.png)
![[Python] 행렬 만들고 연산까지 해보기2 [Python] 행렬 만들고 연산까지 해보기2](https://blog.kakaocdn.net/dn/bhpMcC/btqIGm8DEp8/CwtKFetIlniaHhbiR5vwKk/img.png)

![Python] 선형 연립방정식과 역행렬 — 나의 개발 공부 일지 Python] 선형 연립방정식과 역행렬 — 나의 개발 공부 일지](https://blog.kakaocdn.net/dn/bBMiEQ/btqYuq8tlxa/MXGFA4U60xGhWkkTMEB0M0/img.png)

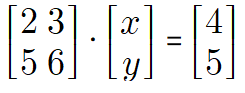

![배열과 행렬] 연립방정식의 해법 - YouTube 배열과 행렬] 연립방정식의 해법 - Youtube](https://i.ytimg.com/vi/6vjvar01YrY/hqdefault.jpg?sqp=-oaymwEmCOADEOgC8quKqQMa8AEB-AH-BIAC4AOKAgwIABABGHIgSSg8MA8=&rs=AOn4CLClFu0lcxYhAJzW7uQbzTDvC_A_-A)



![AI Math] 행렬 Ai Math] 행렬](https://images.velog.io/images/ssu_hyun/post/77d1357a-73ff-4a76-90fa-43f716a6688b/image.png)




![사이킷런 정주행] 1. LinearRegression | 텐서 플로우 블로그 (Tensor ≈ Blog) 사이킷런 정주행] 1. Linearregression | 텐서 플로우 블로그 (Tensor ≈ Blog)](https://tensorflowkorea.files.wordpress.com/2018/11/e18483e185a1e1848be185aee186abe18485e185a9e18483e185b3-1.png)
Article link: 넘파이 역행렬.
주제에 대해 자세히 알아보기 넘파이 역행렬.
- [numpy(넘파이)] 행렬곱(내적), 역행렬 구하기 (+ 역행렬 검증하기)
- Python Numpy.linalg.inv()-역행렬 – Delft Stack
- Numpy 함수로 행렬연산 다루기 – 꼬동의 데스크탑
- 머신 러닝 기본#7 – numpy로 전치행렬, 단위행렬, 역행렬
- [Python] 행렬 만들고 연산까지 해보기2 – 보고의 진땀나는 하루
- [numpy] np.linalg – 파이프마임 – 티스토리
- Matrix(행렬), Pseudo Inverse(의사 역행렬), Numpy
- 넘파이(NumPy) 기초: 배열 및 벡터 계산
- 랭크, 역행렬, 일차방정식 풀이- 요약 (numpy) – 연금술사
- [Python으로 데이터 다루기 I – numpy]2강:Numpy와 선형대수
더보기: blog https://muadacsan3mien.com/tin-tuc