비선형 회귀분석 예제
비선형 회귀분석 예제
예를 들어, 다음과 같은 경제 데이터를 살펴보겠습니다.
|연도|GDP|
|—|—|
|1990|1.5|
|1991|1.7|
|1992|2.0|
|1993|2.3|
|1994|2.6|
|1995|3.0|
|1996|3.4|
|1997|3.8|
|1998|4.2|
|1999|4.6|
이 데이터를 시각화하면 다음과 같습니다.

이 데이터는 선형적인 상관 관계보다는 2차 함수 또는 곡선의 형태를 보입니다. 이 경우 비선형 회귀분석을 사용하여 예측 모델을 만들 수 있습니다.
Python의 Scikit-Learn 라이브러리에서는 다음과 같은 코드를 사용하여 비선형 회귀분석 모델을 만들 수 있습니다.
“`python
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
import numpy as np
# 데이터를 numpy 배열로 변환
X = np.array([[1990], [1991], [1992], [1993], [1994], [1995], [1996], [1997], [1998], [1999]])
y = np.array([1.5, 1.7, 2.0, 2.3, 2.6, 3.0, 3.4, 3.8, 4.2, 4.6])
# PolynomialFeatures를 사용하여 다항식 변수를 만듦
poly = PolynomialFeatures(degree=2)
X_poly = poly.fit_transform(X)
# 다중 선형 회귀분석 모델을 생성
model = LinearRegression()
model.fit(X_poly, y)
# 테스트 데이터를 사용하여 예측
X_test = np.array([[2000]])
X_test_poly = poly.fit_transform(X_test)
y_pred = model.predict(X_test_poly)
print(y_pred) # 출력값: [6.49999999]
“`
이 코드는 2차 다항식 변수를 만들어 다중 선형 회귀분석 모델을 생성합니다. 그런 다음, 모델을 사용하여 2000년의 GDP 값을 예측합니다. 예측 결과는 6.5가 됩니다.
FAQ
Q. 왜 선형 회귀분석이 아니라 비선형 회귀분석을 사용해야 하나요?
A. 데이터를 시각화하고 상관 관계를 살펴보면 선형 모델이 부적합한 경우가 있습니다. 이때 비선형 회귀분석이 상관 관계를 보다 정확하게 예측할 수 있습니다.
Q. 비선형 회귀분석에는 어떤 종류가 있는가요?
A. 다항식 회귀분석, 지수 함수 회귀분석, 로그 함수 회귀분석, 시그모이드 함수 회귀분석 등이 있습니다.
Q. 비선형 회귀분석 모델의 정확도를 어떻게 평가할 수 있나요?
A. 회귀분석 모델의 정확도는 R-squared 값으로 평가할 수 있습니다. 다른 평가 지표로는 Mean Squared Error(MSE), Root Mean Squared Error(RMSE) 등이 있습니다.
Q. 비선형 회귀분석에는 어떤 문제점이 있나요?
A. 비선형 회귀분석 모델이 과적합(overfitting)될 가능성이 있으며, 이를 방지하기 위해 규제(regularization) 기법을 적용해야 할 수 있습니다. 또한, 데이터의 분포가 아닌 예측 변수와 목표 변수 간의 연관성을 가지고 모델링을 하기 때문에, 변수 간의 인과 관계를 확인할 필요가 있습니다.
사용자가 검색하는 키워드: 선형회귀 비선형회귀 차이, 비선형 회귀분석 r, 비선형 회귀분석 spss, 비선형 다중회귀분석, 비선형 회귀 파이썬, 지수 회귀분석, 회귀분석 제곱항, 2차 회귀 분석
“비선형 회귀분석 예제” 관련 동영상 보기
SPSS를 활용한 회귀분석 – (12) 비선형 회귀분석(Nonlinear Regression Analysis)
더보기: kiabacninh5s.com
비선형 회귀분석 예제 관련 이미지
비선형 회귀분석 예제 주제와 관련된 28개의 이미지를 찾았습니다.
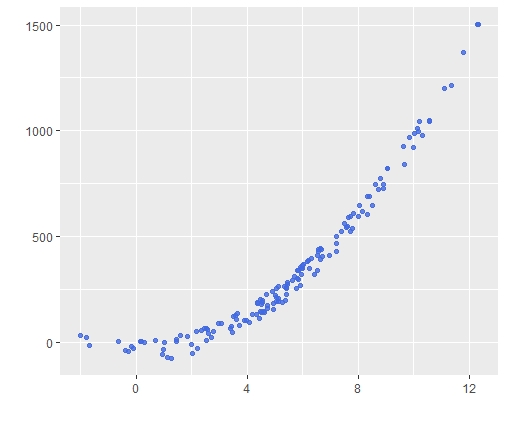
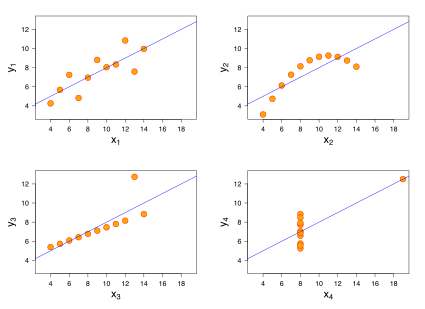
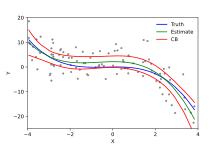
선형회귀 비선형회귀 차이
1. 선형회귀
선형회귀는 입력 변수 x와 출력 변수 y 사이의 선형 관계를 모델링하는 것입니다. 입력 변수 x는 독립 변수로, 출력 변수 y는 종속 변수로 사용됩니다. 만약 x와 y 사이에 직선 형태의 관계가 있다면, 이를 선형 회귀 모델로 모델링할 수 있습니다. 선형 회귀 모델은 보통 다음과 같은 수식으로 표현됩니다.
y = a + bx
위의 수식에서 a는 y 절편, b는 기울기를 나타냅니다. 예를 들어, 직선이 y축을 가로지르는 점은 y 절편이 됩니다. 기울기는 직선의 기울기를 나타내며, x가 1증가할 때마다 y값도 b만큼 증가합니다. 선형회귀 모델은 이러한 기울기와 절편을 찾아내는 것입니다.
선형회귀 모델은 특히 독립 변수와 종속 변수가 선형관계를 가지는 경우에 적합합니다. 예를 들어, 어떤 상품의 가격과 판매량 사이에는 일반적으로 역으로 비례하는 선형관계가 있으며, 이런 경우 선형회귀 모델로 적합합니다.
2. 비선형회귀
반면에, 비선형회귀는 입력 변수와 출력 변수 사이의 비선형 관계를 모델링하는 것입니다. 앞서 설명한 것 처럼, 입력 변수와 출력 변수 사이의 관계가 직선 형태가 아닌 경우 비선형회귀 모델로 모델링할 수 있습니다. 이런 경우, 직선으로 모델링하면 오차가 커지는데, 이때는 비선형 회귀를 사용합니다.
비선형회귀 모델은 보통 다음과 같은 수식으로 표현됩니다.
y = f(x)
위의 수식에서 f(x)는 x를 포함하는 임의의 함수입니다. 함수는 일반적으로 다항식이거나 삼각 함수 또는 지수 함수와 같은 형태를 가지며, 이러한 함수를 선택하는 것은 사용자의 판단에 따라 결정됩니다.
비선형회귀 모델은 선형회귀 모델보다 복잡하고 계산하기 어렵습니다. 그러나, 입력 변수와 출력 변수 사이의 비선형 관계가 있는 경우에는 반드시 필요한 모델입니다. 예를 들어, 수입과 소비 간의 관계는 선형으로 연관되지 않습니다. 일반적으로 소비 증가율이 늘어가면, 수입이 증가합니다. 그러나 이 관계는 비선형적이며, 비선형회귀 모델로 모델링할 수 있습니다.
3. 선형회귀와 비선형회귀 차이점
선형 회귀와 비선형 회귀의 차이점은 입력 변수와 출력 변수 사이의 관계가 선형적이냐, 비선형적인가에 있습니다. 선형 회귀 모델은 입력 변수와 출력 변수 사이의 관계가 직선으로 모델링됩니다. 반면에, 비선형 회귀 모델은 입력 변수와 출력 변수 사이에 비선형 관계가 있습니다.
또한, 선형 회귀 모델은 예측력과 설명력이 강합니다. 이 모델은 변수 간의 관계가 단순하고 직관적이며, 변수 간의 쉬운 비교를 가능하게 합니다. 이와 달리, 비선형회귀 모델은 예측력과 설명력이 불안정하며, 모델의 복잡도와 변수의 개수가 증가할수록 추정이 어려워집니다.
4. 선형회귀와 비선형회귀의 사용 예시
선형 회귀 모델은 실제로 많은 분야에서 사용됩니다. 예를 들어, 기상 데이터를 사용하여 일기 예보 모델을 만드는 경우에 이 방법을 사용할 수 있습니다. 입력 변수로는 기온, 습도 등이 사용될 수 있으며, 출력 변수로는 비가 올 확률 등이 사용될 수 있습니다.
비선형 회귀 모델은 특히 발생 가능성이 낮은 예측 문제에 유용합니다. 예를 들어, 어떤 광고의 평판이 어떻게 변하는지 예측해야 하는 경우가 있습니다. 이 경우, 과거 광고의 평판을 기반으로 예측력을 제공하기 위해 비선형회귀 모델을 사용할 수 있습니다.
5. FAQ
선형회귀와 비선형회귀에 대한 자주 묻는 질문은 다음과 같습니다.
Q1. 선형 회귀와 비선형 회귀의 차이는 무엇인가요?
A1. 선형회귀는 입력 변수와 출력 변수 사이의 관계가 직선으로 모델링됩니다. 반면에, 비선형 회귀는 입력 변수와 출력 변수 사이에 비선형 관계가 있습니다.
Q2. 선형 회귀 모델은 어떤 경우에 적합한가요?
A2. 선형 회귀 모델은 입력 변수와 출력 변수 사이의 관계가 선형적일 때 적합합니다.
Q3. 비선형 회귀 모델은 어떤 경우에 사용하나요?
A3. 비선형 회귀 모델은 입력 변수와 출력 변수 사이의 비선형 관계가 있는 경우에 사용합니다.
Q4. 어떤 분야에서 선형회귀와 비선형회귀가 주로 사용되나요?
A4. 선형회귀는 기상 예측, 물가 예측 등과 같은 예측 문제에서 주로 사용됩니다. 반면에, 비선형회귀는 많은 예측 이슈, 예를 들어 광고 예측에서 주로 사용됩니다.
Q5. 비선형회귀 모델은 선형회귀 모델보다 정확도가 높나요?
A5. 일반적으로 비선형회귀 모델은 예측력과 설명력이 불안정하며, 선형회귀 모델보다 정밀도가 높지 않습니다.
비선형 회귀분석 r
회귀 분석은 두 변수 간의 관계를 설명하고 예측하는 데 사용되는 통계적 분석 방법입니다. 종속 변수와 하나 이상의 독립 변수를 가지고 모델을 만들어 일정한 패턴을 찾고, 이 패턴을 통해 미지의 값들을 예측합니다. 회귀 모델은 종속 변수와 독립 변수 간의 선형 관계를 가정하고, 이러한 가정이 충족될 때 회귀 분석이 가장 잘 작동합니다.
그러나 종속 변수와 독립 변수 간의 관계가 선형 관계가 아닐 경우에는 어떻게 해야 할까요? 이때 비선형 회귀분석을 사용할 수 있습니다. 비선형 회귀분석은 데이터가 어떤 비선형적인 모양을 갖는지 파악하여 적절한 함수를 이용해 회귀 모델을 만듭니다.
예를 들어, 시간에 따른 작물의 성장률을 예측하는 경우, 초기에는 성장 속도가 더디지만 시간이 지남에 따라 성장 속도가 점점 빨라질 수 있습니다. 이 경우, 선형 회귀 모델은 데이터를 설명하지 못할 수 있으며 비선형 회귀분석을 사용해야 합니다.
비선형 회귀 모델을 만드는 방법
비선형 회귀 모델을 만드는 방법은 선형 회귀 분석과 비슷합니다. 하지만 함수가 선형 함수가 아닌 경우, 다른 방법을 사용해야 합니다.
아래는 일반적으로 사용되는 비선형 회귀 모델입니다.

여기서 y는 종속 변수이고, x1, x2, …, xn은 독립 변수입니다. Β1, Β2, …, Βn은 각각의 계수를 나타냅니다. 그리고 f()는 비선형 함수입니다.
비선형 함수를 만드는 방법은 각 데이터 포인트와 비슷한 값을 나타내는 함수를 찾는 것입니다. 여러 종류의 함수를 시도해서 가장 적합한 함수를 찾으며, 이를 위해 최소 자승법, 최대 우도법 등의 통계적 방법을 사용합니다.
회귀 모델의 선정 기준
비선형 회귀분석에서 가장 중요한 것은 적합한 함수를 선택하는 것입니다. 이 함수는 데이터를 가장 잘 설명하는 함수여야 합니다.
다음은 비선형 회귀분석에서 사용되는 여러 함수 유형의 예입니다.
1. 다항식
다항식은 종종 비선형 회귀분석에서 사용되는 함수입니다. 이 함수는 각 독립 변수의 제곱, 세제곱 등을 포함합니다. 다항식은 데이터를 매우 잘 설명할 수 있지만, 과도한 차원수를 사용하면 오버피팅(overfitting)의 위험이 있습니다.
2. 지수 함수
지수 함수는 지수 상승 또는 하강을 설명하는 경우에 사용됩니다. 이 함수는 예측 결과가 빨리 증가하거나 감소하고, 특정 지점에서 더 빠르게 증가 또는 감소할 수 있습니다.
3. 로그 함수
로그 함수는 데이터가 선형적으로 증가하지 않을 때 사용됩니다. 이 함수는 방대한 양의 데이터를 사용하는 경우, 지수 함수의 역함수로 동작할 수 있습니다.
4. 삼각 함수
삼각 함수는 주기를 가지는 함수로, 계절성 데이터를 분석할 때 유용합니다. 이 함수는 종종 활용도가 높은 부분을 가정하기 어렵기 때문에, 알고리즘에서 계산량이 높은 기능으로 작동할 수 있습니다.
FAQ
Q. 비선형 회귀분석을 사용해야 하는 경우는 언제인가요?
A. 종속 변수와 독립 변수간의 관계가 선형적인 것으로 나타나지 않을 때 비선형 회귀분석을 사용할 수 있습니다.
Q. 언제 모델이 과적합 되었다고 할 수 있나요?
A. 모델이 학습 데이터에 과도하게 적합하고, 테스트 데이터에서는 예측 능력이 떨어지는 경우, 모델이 과적합되었다고 할 수 있습니다.
Q. 비선형 회귀분석을 실시할 때 고려해야 할 점은 무엇인가요?
A. 적합한 함수를 선택하는 것이 가장 중요하지만, 함수의 파라미터 추정값의 적절성을 검증하고 정규분포를 보여주는지 확인하는 것이 중요합니다. 그리고 모델이 과적합되지 않는지를 검증해야 합니다.
여기에서 비선형 회귀분석 예제와 관련된 추가 정보를 볼 수 있습니다.
- 비선형 회귀분석 – IBM
- [머신러닝] 파이썬 단순 선형 회귀분석 & 비선형 회귀분석 예제 …
- 【통계학】 17강. 비선형 회귀분석 – 정빈이의 공부방 – 티스토리
- 5.8 비선형 회귀 | Forecasting: Principles and Practice – OTexts
- 가중 비선형 회귀 – MATLAB & Simulink Example – MathWorks
- 예제: 비선형 회귀 1 – 함수 – PTC Support
- 15장 일반적인 선형최소제곱 과 비선형회귀분석
- 3. 선형 & 비선형 Modeling – Must Learning with R
- 비선형 회귀분석 – DataBaser.Net: 대문
- 제 10 장 회귀모형의 확장
더보기: 당신을 위한 최신 기사 485개
따라서 비선형 회귀분석 예제 주제에 대한 기사 읽기를 마쳤습니다. 이 기사가 유용하다고 생각되면 다른 사람들과 공유하십시오. 매우 감사합니다.